大O符号
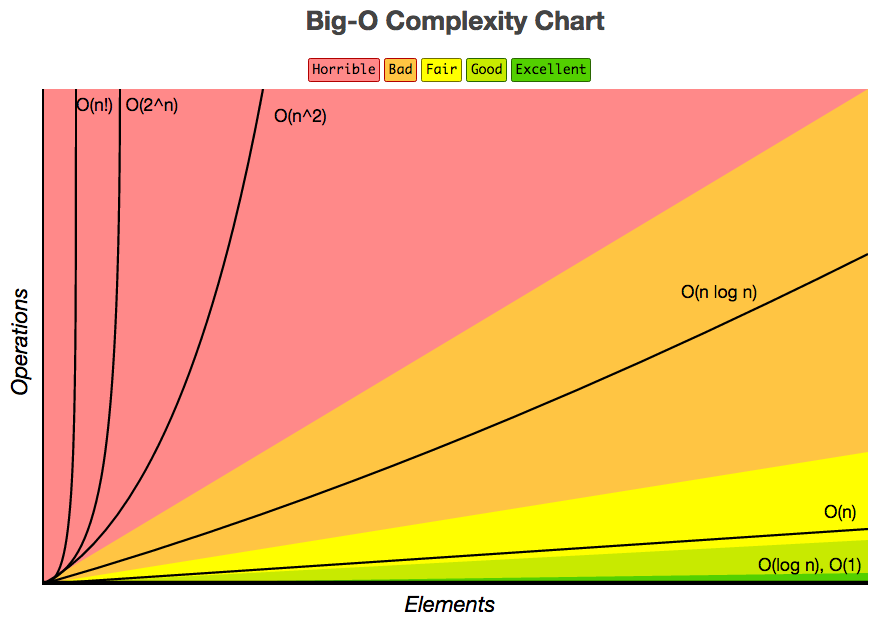
大O符号(Big-O notation)是用于描述函数渐近行为的数学符号。它用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。下图展示了算法分析中一些常见的增长曲线。
数组排序
| Algorithm |
Categories |
Stability |
Time Complexity |
Space Complexity |
| Best |
Average |
Worst |
Worst |
| Quicksort |
Exchange sorts |
unstable |
Ω(n log(n)) |
Θ(n log(n)) |
O(n^2) |
O(n) / O(log(n)) |
| Mergesort |
Merge sorts |
stable |
Ω(n log(n)) |
Θ(n log(n)) |
O(n log(n)) |
O(n) |
| Timsort |
Hybrid sorts |
stable |
Ω(n) |
Θ(n log(n)) |
O(n log(n)) |
O(n) |
| Heapsort |
Selection sorts |
unstable |
Ω(n log(n)) |
Θ(n log(n)) |
O(n log(n)) |
O(1) |
| Bubble Sort |
Exchange sorts |
stable |
Ω(n) |
Θ(n^2) |
O(n^2) |
O(1) |
| Insertion Sort |
Insertion sorts |
stable |
Ω(n) |
Θ(n^2) |
O(n^2) |
O(1) |
| Selection Sort |
Selection sorts |
unstable |
Ω(n^2) |
Θ(n^2) |
O(n^2) |
O(1) |
| Shell Sort |
Insertion sorts |
unstable |
Ω(n log(n)) |
Θ(n(log(n))^2) |
O(n(log(n))^2) |
O(1) |
| Bucket Sort |
Distribution sorts |
stable |
Ω(n+k) |
Θ(n+k) |
O(n^2) |
O(nk) / O(n) |
| Radix Sort |
Distribution sorts |
stable |
Ω(nk) |
Θ(nk) |
O(nk) |
O(n+k) |
| Counting Sort |
Distribution sorts |
stable |
Ω(n+k) |
Θ(n+k) |
O(n+k) |
O(k) |
| Cubesort |
- |
stable |
Ω(n) |
Θ(n log(n)) |
O(n log(n)) |
O(n) |
数据结构操作
通用数据结构
| Data Structure |
Time Complexity |
Space Complexity |
| Average |
Worst |
Worst |
| Access |
Search |
Insertion |
Deletion |
Access |
Search |
Insertion |
Deletion |
|
| Array |
Θ(1) |
Θ(n) |
Θ(n) / O(1) |
Θ(n) / O(1) |
O(1) |
O(n) |
O(n) / O(1) |
O(n) / O(1) |
O(n) |
| Stack |
Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
| Queue |
Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
| Singly-Linked List |
Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
| Doubly-Linked List |
Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
| Skip List |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n) |
O(n) |
O(n log(n)) |
| Hash Table |
N/A |
Θ(1) |
Θ(1) |
Θ(1) |
N/A |
O(n) |
O(n) |
O(n) |
O(n) |
| Binary Search Tree |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n) |
O(n) |
O(n) |
| Cartesian Tree |
N/A |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
N/A |
O(n) |
O(n) |
O(n) |
O(n) |
| B-Tree |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
| Red-Black Tree |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
| Splay Tree |
N/A |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
N/A |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
| AVL Tree |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
| KD Tree |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n) |
O(n) |
O(n) |
堆
| Heaps |
Time Complexity |
| Heapify |
Find Max |
Extract Max |
Increase Key |
Insert |
Delete |
Merge |
| Sorted LinkedList |
- |
O(1) |
O(1) |
O(n) |
O(n) |
O(1) |
O(m+n) |
| Unsorted Linked List |
- |
O(n) |
O(n) |
O(1) |
O(1) |
O(1) |
O(1) |
| Binary Heap |
O(n) |
O(1) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(m+n) |
| Binomial Heap |
- |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
| Fibonacci Heap |
- |
O(1) |
O(log(n)) |
O(1) |
O(1) |
O(log(n)) |
O(1) |
图
| Node / Edge Management |
Storage |
Add Vertex |
Add Edge |
Remove V ertex |
Remove Edge |
Query |
| Adjacency List |
O(|V|+|E|) |
O(1) |
O(1) |
O(|V| + |E|) |
O(|E|) |
O(|V|) |
| Incidence List |
O(|V|+|E|) |
O(1) |
O(1) |
O(|E|) |
O(|E|) |
O(|E|) |
| Adjacency Matrix |
O(|V|^2) |
O(|V|^2) |
O(1) |
O(|V|^2) |
O(1) |
O(1) |
| Incidence Matrix |
O(|V| ⋅ |E|) |
O(|V| ⋅ |E|) |
O(|V| ⋅ |E|) |
O(|V| ⋅ |E|) |
O(|V| ⋅ |E|) |
O(|E|) |
查找算法
| Algorithm |
Data Structure |
Time Complexity |
Space Complexity |
| Average |
Worst |
Worst |
| Depth First Search |
Graph of |V|vertices and |E|edges |
- |
O(|E| + |V|) |
O(|V|) |
| Breadth First Search |
Graph of |V|vertices and |E|edges |
- |
O(|E| + |V|) |
O(|V|) |
| Binary Search |
Sorted array of nelements |
O(log(n)) |
O(log(n)) |
O(1) |
| Brute Force |
Array |
O(n) |
O(n) |
O(1) |
| Shortest path by Bellman-Ford |
Graph with |V|vertices and |E|edges |
O(|V||E|) |
O(|V||E|) |
O(|V|) |
REFERENCE
http://www.bigocheatsheet.com/
http://en.wikipedia.org/wiki/Array_data_structure
http://en.wikipedia.org/wiki/Singly_linked_list#Singly_linked_lists
http://en.wikipedia.org/wiki/Doubly_linked_list
http://en.wikipedia.org/wiki/Skip_list
http://en.wikipedia.org/wiki/Hash_table
http://en.wikipedia.org/wiki/Binary_search_tree
http://en.wikipedia.org/wiki/Quicksort
http://en.wikipedia.org/wiki/Merge_sort
http://en.wikipedia.org/wiki/Timsort
http://en.wikipedia.org/wiki/Heapsort
http://en.wikipedia.org/wiki/Bubble_sort
http://en.wikipedia.org/wiki/Insertion_sort
http://en.wikipedia.org/wiki/Selection_sort
http://en.wikipedia.org/wiki/Bucket_sort
http://en.wikipedia.org/wiki/Radix_sort
http://en.wikipedia.org/wiki/Adjacency_list
http://en.wikipedia.org/wiki/Incidence_list
http://en.wikipedia.org/wiki/Incidence_matrix
http://en.wikipedia.org/wiki/Adjacency_matrix
http://en.wikipedia.org/wiki/Linked_list
http://en.wikipedia.org/wiki/Binary_heap
http://en.wikipedia.org/wiki/Binomial_heap
http://en.wikipedia.org/wiki/Fibonacci_heap
