在计算机中,三维空间中点的位置可以用三坐标表示,此处用一个矢量来保存某一点的坐标。一个几何体可以看做是由很多点构成的,而其中的每个点都可以用以下的矢量表示:
$$ \begin{bmatrix} x \\ y \\ z\\ \end{bmatrix} $$而对其进行的各种变换(平移、缩放、旋转等)均可以用矩阵来表达,对基矢量组成的矩阵进行变换得到变换后的矩阵即可作为任意矢量进行相应坐标变换的变换矩阵。本文中使用的坐标系为左手坐标系(left-hand rule)。
若使用$a$表示变换前的坐标,$b$表示变换之后的坐标,$F$表示变换操作(事实上是可以表示广义的函数映射),则可以写成以下形式: $$ F(a) = b $$ 如果对于任意的变量$a$、$b$和任意数$k$满足: $$ F(a+b) = F(a) + F(b) \\ F(ka) = kF(a) $$ 则称 $F$为线性变换,除投影外,经过线性变换的平行线仍为平行线,线性变换保留直线和平行线,且不会移动原点。线性变换主要包括旋转(绕原点)、缩放、投影(正交)、镜像和切变等。旋转
在线性变换中,旋转操作不会改变原点的位置,即旋转中心为原点或转轴经过原点。
2D中的旋转
2D环境中物体绕原点旋转角度$\theta$(逆时针方向为正),根据旋转基矢量来推出变换矩阵: 基矢量: $$ \begin{bmatrix} p\\ q \end{bmatrix} = \begin{bmatrix} 1&0 \\ 0&1 \\ \end{bmatrix} $$ 旋转之后得到$v'$:
绕坐标轴的旋转
绕$x$轴的旋转,根据旋转之后的基矢量容易得出旋转变换矩阵为: $$ R_x(\theta) = \begin{bmatrix} p' \\ q' \\ r' \end{bmatrix} = \begin{bmatrix} 1& 0 & 0 \\ 0&\cos\theta& \sin\theta\\ 0&-\sin\theta& \cos\theta \end{bmatrix} $$ 同理可得绕$y$轴和$z$轴的变换矩阵: $$ R_y(\theta) = \begin{bmatrix} p' \\ q' \\ r' \end{bmatrix} = \begin{bmatrix} \cos\theta& 0 & -\sin\theta\\ 0&1&0 \\ \sin\theta&0& \cos\theta \end{bmatrix} , R_z(\theta) = \begin{bmatrix} p' \\ q' \\ r' \end{bmatrix} = \begin{bmatrix} \cos\theta& \sin\theta & 0\\ -\sin\theta& \cos\theta &0 \\ 0&0&1 \end{bmatrix} $$绕任意轴的旋转
使用$n$来表示旋转的轴,则由$v$绕轴$n$旋转角度$\theta$得到$v'$可表示为: $$ vR(n,\theta)=v' $$ 为推算出变换矩阵$R$,此处可以将空间中任意矢量$v$分解为$v_\parallel$和$v_\perp$,其中$v_\parallel$表示$v$平行于$n$的分量,$v_\perp$表示$v$垂直于$n$的分量,则有: $$ v=v_\parallel + v_\perp $$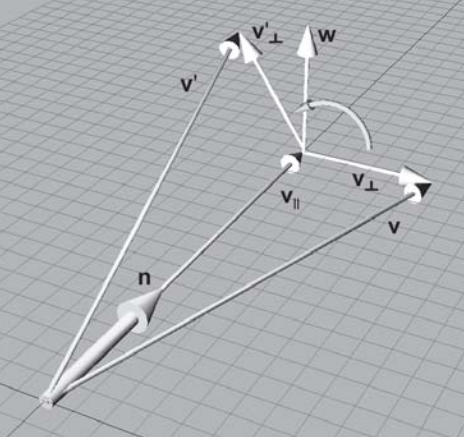
缩放
本文讨论的缩放均以原点为中心。
可以指定比例因子$k$来使物体据此放大或缩小。如果在各个方向的比例因子一样则称之为均匀缩放,均匀缩放可保持物体的角度和比例不变。如果需要“挤压”或“拉伸”物体,则在不同方向应用不同的比例因子即可,这称为费均匀缩放。非均匀缩放时,物体的角度将发生变化。非均匀缩放的效果类似于切变。
如果$|k|<1$,物体将变小或变短,如果$|k|>1$,物体将变大或变长。如果$|k|=0$,就是正交投影,如果$|k|<0$,就是镜像。本节先讨论$|k|>0$的情况。沿坐标轴方向的缩放
先看2D情况,基矢量: $$ \begin{bmatrix} p\\ q \end{bmatrix} = \begin{bmatrix} 1&0 \\ 0&1 \\ \end{bmatrix} $$ 对$x$轴和$y$轴使用缩放因子$k_x$和$k_y$之后有: $$ p'=k_xp = k_x\begin{bmatrix}1 & 0\end{bmatrix} = \begin{bmatrix}k_x & 0\end{bmatrix} \\ q'=k_yq = k_y\begin{bmatrix}0 &1\end{bmatrix} = \begin{bmatrix}0 & k_y\end{bmatrix} $$ 所以2D缩放矩阵: $$ S(k_x,k_y) = \begin{bmatrix} p'\\ q' \end{bmatrix} = \begin{bmatrix} k_x&0 \\ 0&k_y \end{bmatrix} $$ 易得3D中增加缩放因子$k_z$后的缩放矩阵为: $$ S(k_x,k_y,k_z) = \begin{bmatrix} k_x&0 & 0\\ 0&k_y & 0\\ 0 & 0 & k_z \end{bmatrix} $$沿任意方向的缩放
首先考虑2D情况,$n$为平行于缩放方向的单位矢量,$k$为缩放因子,缩放沿穿过原点并平行于$n$的直线(3D中为平面)进行。 与之前推导旋转公式时相同,将$v$分解为$v_\parallel$和$v_\perp$,其中$v_\parallel$表示$v$平行于$n$的分量,$v_\perp$表示$v$垂直于$n$的分量: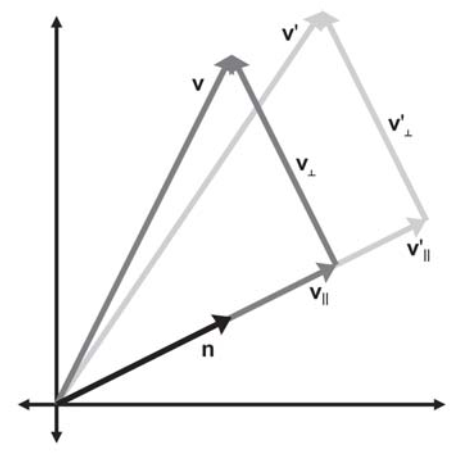
投影(正交)
向坐标轴或平面上投影
向坐标轴或平面投影在实际中不常发生,大多数情况是向低维的变量赋值,且要抛弃维数时。如将3D点赋值给2D点,抛弃$z$分量,只复制$x$和$y$。结合上一节内容,使垂直方向上的缩放因子为0即可实现向坐标轴或平面投影: $$ P_x = S(\begin{bmatrix}0 &1\end{bmatrix},0) = \begin{bmatrix}1 &0 \\ 0 & 0 \end{bmatrix} \\ P_y = S(\begin{bmatrix}1 &0\end{bmatrix},0) = \begin{bmatrix}0 &0 \\ 0 & 1 \end{bmatrix} \\ P_{xy} = S(\begin{bmatrix}0 &0&1\end{bmatrix},0) = \begin{bmatrix}1&0 &0 \\ 0 & 1 &0 \\ 0 & 0 & 0 \end{bmatrix} \\ P_{xz} = S(\begin{bmatrix}0 &1&0\end{bmatrix},0) = \begin{bmatrix}1&0 &0 \\ 0 & 0 &0 \\ 0 & 0 & 1 \end{bmatrix} \\ P_{yz} = S(\begin{bmatrix}1 &0&0\end{bmatrix},0) = \begin{bmatrix}0&0 &0 \\ 0 & 1 &0 \\ 0 & 0 &1 \end{bmatrix} \\ $$向任意直线或平面投影
此处讨论的任意直线及平面必须通过原点,投影由垂直于直线锪平面的单位矢量$n$定义,使该方向的缩放因子为0即可: $$ P(n) = S(n,0) = \begin{bmatrix} 1-n_x^2 & -n_xn_y\\ -n_xn_y & 1-n_y^2 \end{bmatrix}\\ P(n)=S(n,0) = \begin{bmatrix} 1-n_x^2 & -n_xn_y & -n_xn_z\\ -n_xn_y & 1-n_y^2 &-n_yn_z \\ -n_xn_z &-n_zn_y & 1-n_z^2 \end{bmatrix} $$镜像
镜像(Reflection)使物体沿直线(2D中)或平面(3D中)翻转,使缩放因子为-1即可达到镜像变换的效果: $$ R(n) = S(n,-1)= \begin{bmatrix} 1-2n_x^2 & -2n_xn_y\\ -2n_xn_y & 1-2n_y^2 \end{bmatrix} \\ R(n) = S(n,-1)= \begin{bmatrix} 1-2n_x^2 & -2n_xn_y & -2n_xn_z\\ -2n_xn_y &1-2n_y^2 & -2n_yn_z \\ -2n_xn_z &-2n_zn_y & 1-2n_z^2 \end{bmatrix} $$切变
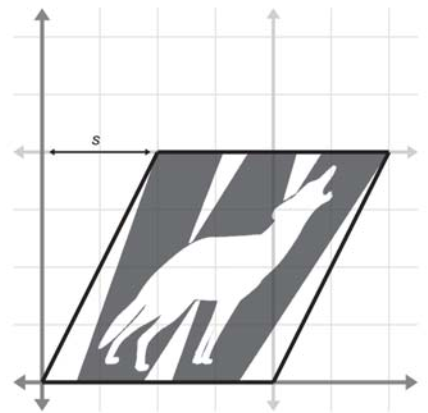
切变(Shearing)是一种坐标系扭曲变换,而非均匀地拉伸。切变发生时,角度会发生变化,但面积和体积会保持不变,基本思想是将某一坐标的乘积加到另一个上。如下图是将$y$乘以某因子然后加到$x$上,得到$x’=x+sy$。